An interesting probability question: Gambler's Ruin
Okay here comes a nice question on probability. (Please mind your random steps =))
Problem:
There are 2 gamblers. Joe has 10 dollars in his pocket and Peter has 2 dollars. They always play with 1$ each game. We know that Peter is better than Joe when it comes to dices he has a probability of winning 2/3. If they play till one of them goes bankrupt what is the chance that Joe will win?
Solution:
From Peter’s point of view this problem is a random walk. We step +1 with a probability of 2/3 and -1 with 1/3 probability. Random walk starts from 2 and will end either at 0 or 12. For a more general solution let’s assign winning probability to p = 2/3 (Peter wins) and j=1/3, M=2 and N=10.
Now let’s say that Peter’s probability of stepping back is $P_{X}$ when his money equals X including all paths(i.e 1 forward 2 backward). For a moment let’s say Joe has infinite money. Assuming M→∞ having a step back does not depend on the location X. Thus
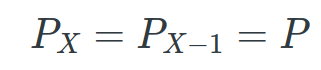
Now let’s find P. The probability of ever stepping back is either step back directly or step forward once and step back twice. So
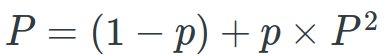
The solution of this equation forms the following graph.
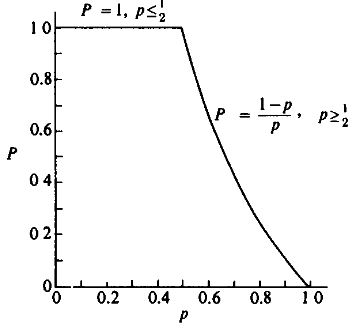
This is actually very interesting. In this conditions, for Peter to lose, he needs to step back N times which is of probability ((1-p)/p)^ N) otherwise games just never ends.
So Peter loses with probability ((1-p)/p)^N) $. Of all his losts there are 2 possibilities. Either he reaches M+N and loses or never reach there. If the probability of never reaching there (Joe winning) is Q, then.
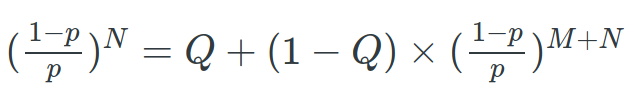
Now we got everything.
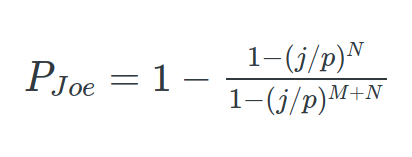
Fantastic, now plug in the numbers.
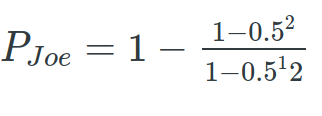
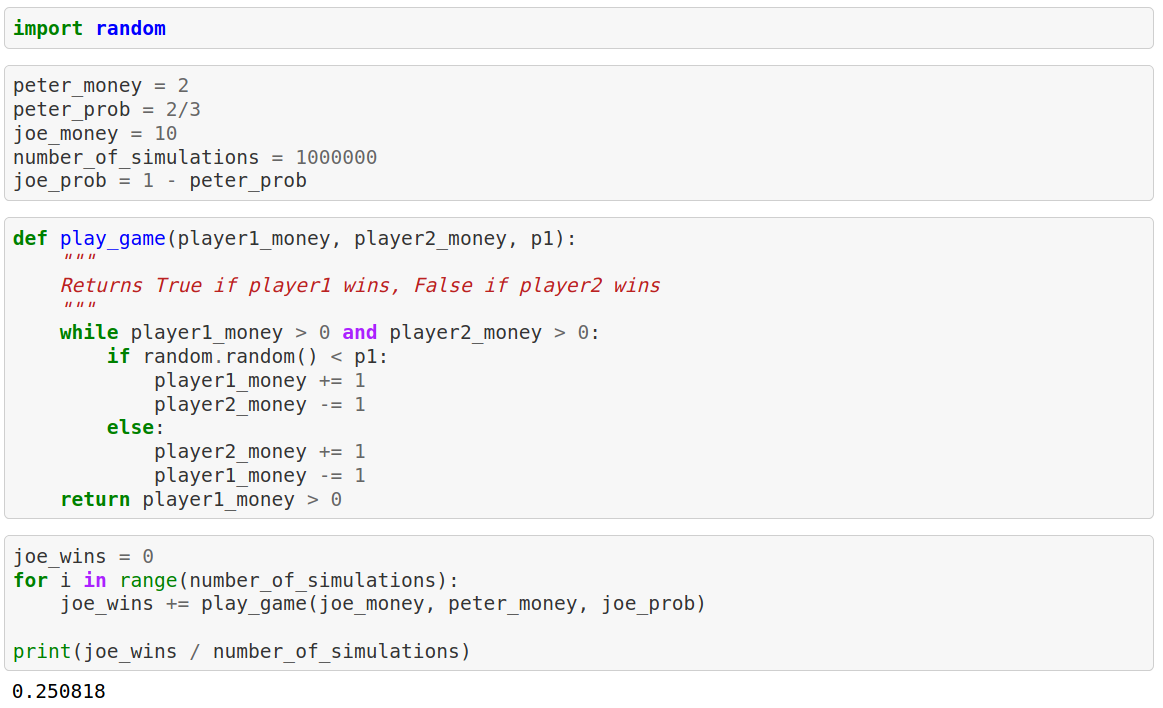
More than you would expect right? Okay now let’s make a Monte Carlo simulation to confirm this result.
 See also:
See also: