Recently I read about a nice probability question and was thrilled about it. It is not that the question is hard but it is because the question really teach about a fundamental issue in probability. So I wanted to both solve the problem and do a Monte Carlo simulation to verify.

Problem:

  • There are cereal boxes numbered 1 to 5 only possible to see after opening the box. A set of one of each number is required to win a price. Knowing that each number is equally likely, how many boxes on average are required to make a complete set?

Solution:

The trick in this question is to define the problem in a nice way using a mathematical description.

Let’s say $T_{1}$ is the number of boxes it takes to get first distinct number and $T_{2}$ is the number of boxes it takes to get the second distinct number after getting the first one. Thus if $T_{win}$ is the number of boxes to get the prize,

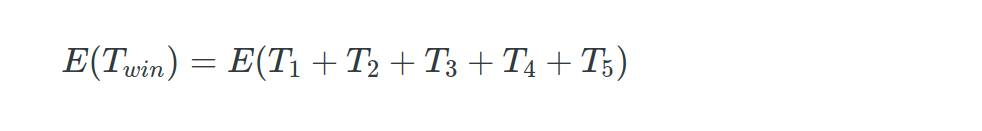
Here it is important to see that $T_1, T_2, T_3, T_4, T_5$ are independent. Thus

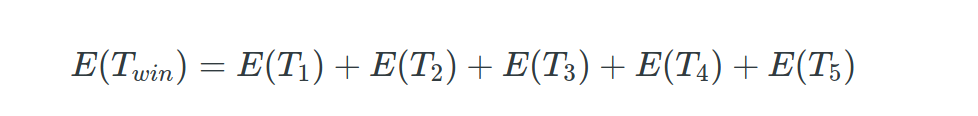
Also note that each of this random variables are coming from a geometrical distribution. I.e

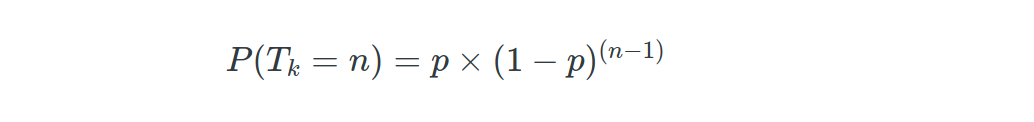
where p = 4/5 for k=2,  p=3/5 for k=3, p=2/5 for k=4 and p=1/5 for k=5.

Since expected value of a geometric random variable is 1/p,

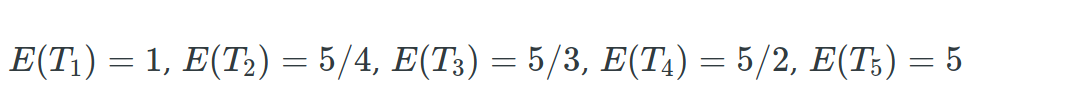
Thus,

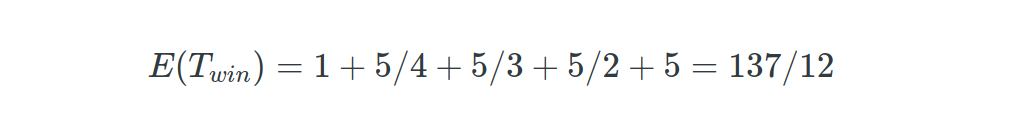
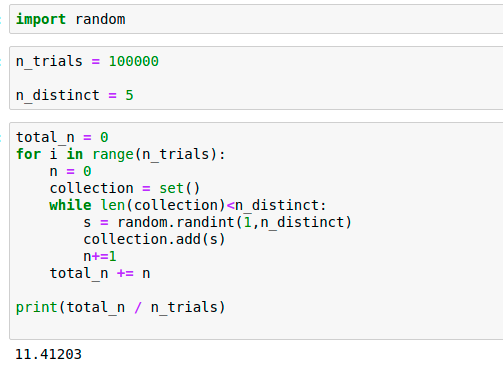
Simulation:

Let’s code this up!

See also:

Code

https://en.wikipedia.org/wiki/Geometric_distribution